複雜度不低於Ω(log²k)
任意度量空間消耗下限
而具體到這項研究,作者利用隨機性和對稱性
定義了一個新的序列ρ(w)
,並
假設
在度量空間M(w)中,對隨機的ρ(w),確定性算法的消耗下限爲Ω(w²)。
首先對於M(0),確定性算法的消耗下限爲1,此時結論成立。
然後試着將w推廣到w+1,構建出M(w+1)的度量空間,它包含兩條由多個M(w)組成的對稱路徑。
在請求ρ(w+1)上,假設此時位於左路徑,下一段位於左右路徑的概率各爲1/2。
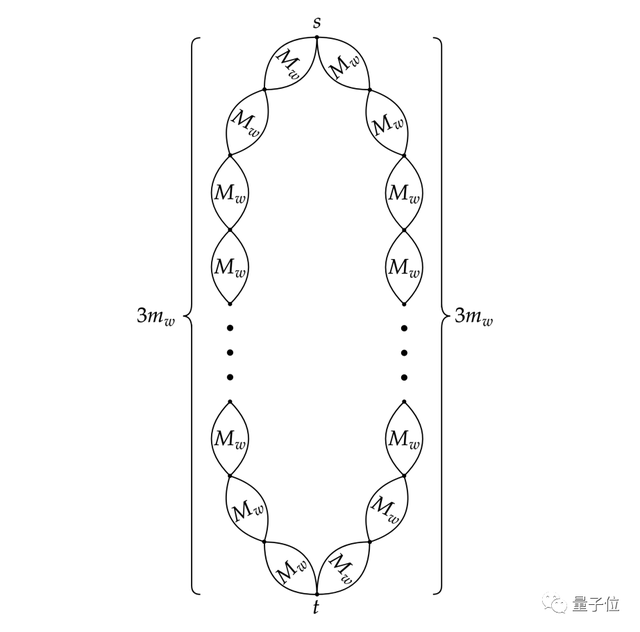
如果下階段位於右路徑,算法複雜度將會因爲路徑切換而升高,不是低消耗。
而如果位於左路徑,由於路徑上都是一個個M(w),所以新增部分的消耗下限就是Ω(w²)(此爲歸納法假設)。
於是對於w+1段路徑,可以將每一段的消耗Ω(w²)累加,即爲(w+1)Ω(w²),結合Ω的定義,最終可以證明M(w+1)的最低消耗爲Ω((w+1)²),進而證明假設成立。
回到最初的度量空間
而作者構建的M(w+1)都是由6個M(w)組成,則M(w)的大小n=|M(w)|=O(6^w),取對數得log|M(w)|=w·log6。

代入Ω(w²)中,得到在n點度量空間中,消耗下限爲Ω((logn/log6)²),而當n=k時,消耗下限則爲Ω((logk/log6)²)。
而log6爲一個2到3之間的常數,除以這樣一個數不會帶來結果的顯著改變,也就證明了k-server問題中消耗不低於Ω(log²k)的結論。
當k足夠大時,log²k顯然大於logk,因此在這樣的k-server問題中,實現O(logk)級別的低消耗是不可能的。
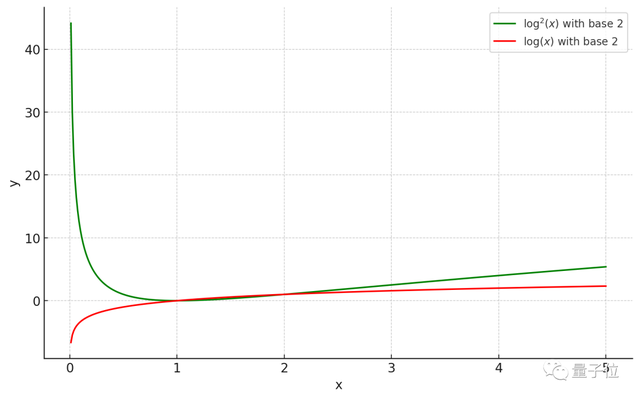
而此前人們一直認爲可以用這樣的消耗解決所有的k-server問題,因此反例的出現便宣告了這一設想的終結。
論文地址:
https://dl.acm.org/doi/pdf/10.1145/3564246.3585132
參考鏈接:
https://www.quantamagazine.org/researchers-refute-a-widespread-belief-about-online-algorithms-20231120/
如若转载,请注明出处:https://www.tuio.cc/479.html



